Functions
Assumed Knowledge
Learning Outcomes
- Know the syntax of functions
- Understand how functions relate to algorithms
- Be able to pass values into a function
- Be able to get values back from a function
- Be able to write your own functions
- Be able to reason about the flow of a program that uses functions
A function is a named piece of code that can be supplied with some inputs (known as parameters) and may return a value back to the caller.
Chapter 7 of Learning Processing by Danel Shiffman.
Macquarie University Videos
Function Design
Function Defintion and Call
Videos by Daniel Shiffman
Discussion
A function is a named piece of code with zero or more inputs that optionally returns a value back to the caller.
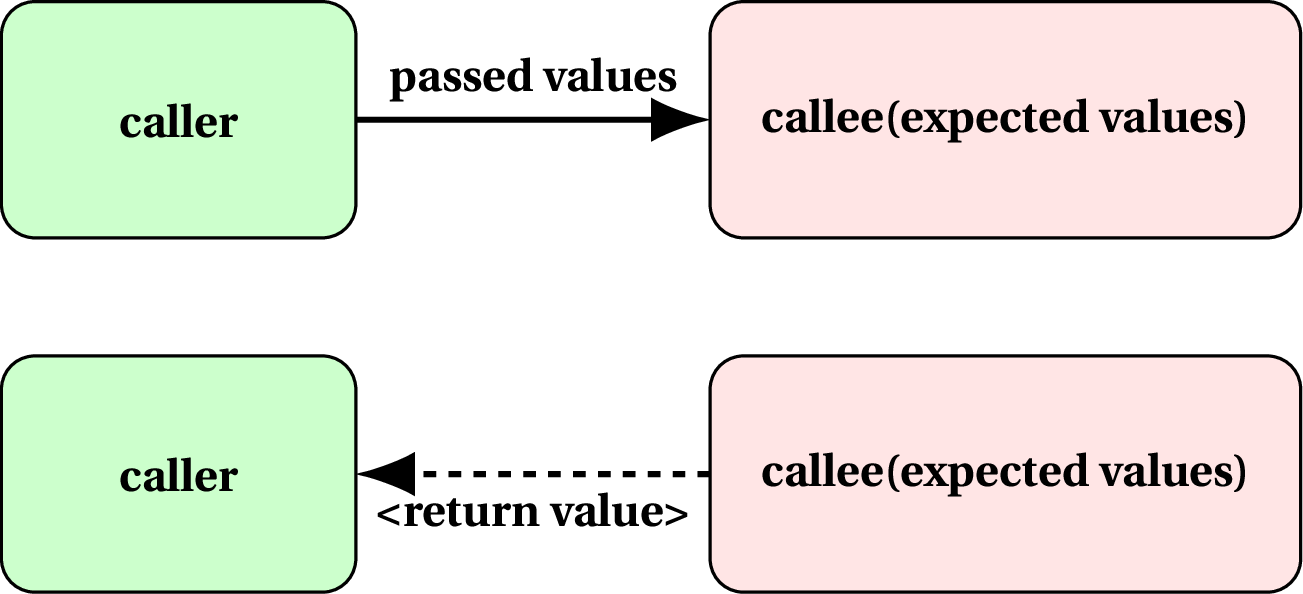
Designing a function
While designing a function, you must think of three aspects carefully:
- Input(s)
- Purpose (decides the name of the function)
- Return value (Type of answer)
Example 1
1
2
3
4
Alice -> Bob: Is 5 an even number?
Bob --> Alice: No.
Charles -> Bob: Is -18 an even number?
Bob --> Charles: Yes.
Here, “Bob” is the function that expects an integer value to be supplied to them, and gives the answer “Yes”/”No” back to the client (caller).
- Input:
int - Purpose:
isEven - Return value: boolean
Example 2
1
2
3
4
5
6
7
8
Alice -> Bob: What is 12.8 rounded-off to the nearest integer?
Bob --> Alice: 13.
Charles -> Bob: What is -3.01 rounded-off to the nearest integer?
Bob --> Charles: -3.
Diane -> Bob: What is "Super Nintendo Chalmers" rounded-off to the nearest integer?
Bob --> Diane: GO AWAY!
Elise -> Bob: What are 1.5 and -2.7 rounded-off to the nearest integer?
Bob --> Elise: One number at a time, please.
Here, we have intentionally made invalid calls from Diane (and Elise) to Bob. This shows that Bob expects one (and only one) float to be provided.
- Input:
float - Purpose:
roundedOff - Return value:
int
Defining a function
All functions have just one function definition - the place that the function itself is described. Syntax of a function definition is:
1
2
3
4
5
6
7
8
returnType function(<parameters>) {
<some code>
<if>
<return statement>
<endif>
<some code>
<return statement>
}
Once this exists, you can have many function calls - the place that the code asks the function to run. Syntax of a function call is:
functionName (<parameters>);
For example, the following function definition
int foo(int a, int b){
int result = a + b;
return result;
}
can be called by anywhere in the program. For example,
void setup() {
int y = foo(12, 5);
}
During the call foo(12, 5),
- Function
fooexpects two integers - The values passed are 12 and 5 (2 integers). So it’s all good
- 12 is copied into the local variable
a - 5 is copied into the local variable
b - Control is transferred to the function
resultbecomes 17.- This value 17 is returned by the function and replaces the call
foo(12, 5). - Control transfers back to the calling statement.
- The statement becomes
int y = 17;since the call is replaced by the value it returns.
Formal and Actual parameters
Since we have both function definitions and function calls, and parameters appear in each, it is useful to be able to distinguish the two uses.
- Parameters appearing in the top line (signature) of a function definition are called formal parameters and are defined in the same way as any other variable declaration. In the example above,
aandbare the formal parameters. - Parameters appearing in a function call are called actual paramters and work like any other value in Processing. In the example above, 12 and 5 are the actual parameters.
When the function is executed, the actual paramters are copied into the formal paramter slots and the function is run.
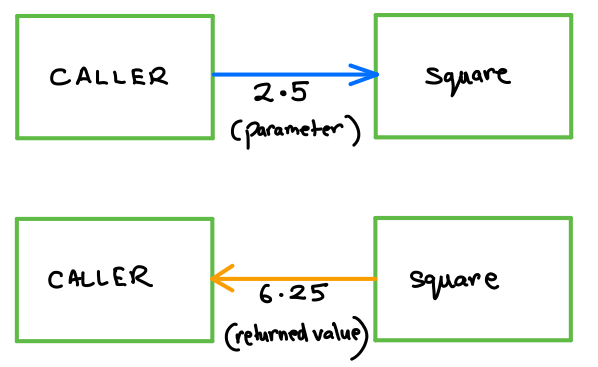
Suppose we have a function that accepts a real number (float) and returns its square.
Draw a block diagram for the interaction when a caller calls the function with the value 2.5. Assume the name of the formal parameter is val, and the value returned by the function is copied into a variable sqr.
Solution
Consider the following function definition,
1
2
3
int roundOff(float a) {
return (int)(a+0.5);
}
Write a statement that calls the function roundOff with the parameter 6.8 and stores the value returned in a variable result.
Solution
1
2
int result;
result = roundOff(6.8);
Which of the following are valid calls to function roundOff?
int a = roundOff(4.5);int b = roundOff(8);roundOff(2.6);float c = roundOff(-1.53);int d = roundOff(3.2, 4.8);int e = roundOff();int e = roundOff(true);
Solution
- Yes
- Yes, the integer is treated like a float when it arrives in the formal parameter. It is identical to writing
float a = 8 - Yes, the return value is thrown away, but that is allowed
- Yes, the return value is treated like a float when it arrives in
c - No, too many actual parameters
- No, not enough acutal parameters
- No, actual parameter type does not match formal parameter type.
Define a function that when passed two integers, returns their average. Remember that 15/2 is 7 while 15/2.0 is 7.5.
Solution
1
2
3
float average(int a, int b){
return (a + b)/2.0;
}
void functions
Functions that perform some action (like drawing something or displaying some text) but don’t return a value have a return type of void. They can still have a return; statement, that transfers control back to the caller.
For example,
void drawShip() {
//IMPORTANT: should draw the ship ONLY if mouse is in the right half
if(mouseX < width/2) { //no need to draw
return; //transfer control back to the caller
}
line(mouseX+50, mouseY-20, mouseX+50, mouseY+10);
triangle(mouseX, mouseY, mouseX+100, mouseY, mouseX+50, mouseY+20);
//control automatically transferred once you reach the end
///so no need to have return statement
}
and the call,
void draw() {
background(255);
drawShip();
}
Effectively unconditional return
A function that promises to return a value, must do so effectively unconditionally.
Take the following example,
boolean isEven(int n) {
if(n%2 == 0) {
return true;
}
if(n%2 != 0) {
return false;
}
}
While mathematically, one of the two boolean expressions (n%2 == 0 and n%2 != 0) WILL be true, the programming language doesn’t make that optimization. For JavaProcessing, the two return statements are in conditional blocks. Hence, you will get a compilation error - method must return a value of type boolean.
To fix this, you should use,
boolean isEven(int n) {
if(n%2 == 0) {
return true;
}
else {
return false;
}
}
Now, in terms of programming, either the if block, or the else block are guaranteed to execute, thereby returning a value unconditionally.
Statements or Expressions?
- function declarations are statements.
- function calls are statements if the function returns
void. - function calls are statements and expressions if they return a value.
- formal parameters are statements.
- actual parameters are expressions.
The fact that a function call in processing can do something and also evaluate to a value makes them special. In fact, this double-life is a bit of a point of friction in language design. Some languages insist that functions must be statements and others insist they must be expressions, but those are rare. The situation we have here, while strange, is quite common.
Furthering your Understanding
Number of digits in an integer
Define a function that when passed an integer, returns the number of digits in the integer.
Solution
1
2
3
4
5
6
7
8
int digits(int input){
int totalSoFar = 0;
while (input > 0) {
totalSoFar++;
intput = input / 10;
}
return totalSoFar;
}
Is Divisible
Given two integers (store in formal parameters a, b), define a function that determines if either of them is divisible by the other. Some input-output mappings are:
a = 14, b = 6–> returnfalsea = 14, b = 7–> returntruea = 9, b = 30–> returnfalsea = 9, b = 36–> returntruea = 12, b = 0–> returntrue(0 is divisible by 12)
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
We need to check if divisible both ways. That is, a % b and b % a.
Notice, that taking modulus 0 of a number will crash our program with a "ArithmeticException: / by zero" error.
We need to only apply the modulus after ensuring the number is not 0 to circumvent that.
*/
boolean isDivisible(int a, int b){
if(b!=0 && a%b==0) {
return true;
}
if(a!=0 && b%a==0) {
return true;
}
return false;
}
Leap Years
A year is leap if it satisfies one of the two conditions,
- it’s divisible by 400, or,
- it’s divisible by 4 but NOT by 100.
Define a function that determines if an year passed (store in formal parameter year) is leap. Return true if it’s a leap year, and false otherwise. Some input-output mappings are:
year = 2016–> returntrueyear = 1800–> returnfalseyear = 2018–> returnfalseyear = 1600–> returntrue
Solution
1
2
3
boolean isLeapYear(int year){
return (isDivisible(year, 400) || (isDivisible(year, 4) && !isDivisible(year 100)));
}
Non-trivial divisors
I would like to count the number of non-trivial (apart from 1 and itself) divisors of a given integer. Some input-output mappings are:
n = 18–> return4(as there are 4 non-trivial divisors: 2, 3, 6, 9)n = 31–> return0(as there is no non-trivial divisor of 31)n = 77–> return2(as there are 2 non-trivial divisors: 7, 11)
Solution
1
2
3
4
5
6
7
8
9
int divisors(int input){
found = 0;
for(int i = 2; i < input; i++){
if (isDivisible(input, i){
found++;
}
}
return found;
}