Sorting
Assumed Knowledge
Learning Outcomes
- Understand why data needs to be sorted
- Understand how data can be sorted
Author: Gaurav Gupta and Greg Baker
Why perform sorting?
Sorting is a fundamental operation that,
- improves the efficiency of several tasks, and,
- makes several other non-trivial tasks, well, trivial.
- is often tested during job interviews
Example 1: Finding the k-highest item in a collection
For an unsorted collection, you have to go through each item of the collection in order to get the first highest value, then again for second highest, etc.
For a sorted collection, the highest value will either be the first value or the last value. The k-highest is at the kth position. Thus, it reduces to a single-operation task.
Example 2: Search
Instead of starting at the beginning and checking every element in a array, if it is sorted, you can jump into the middle of the array and ask whether the element you are looking for is bigger or smaller. That tells you you only need to search half as many elements.
Then you can jump into the half way point of the ones you need to search and repeat the process.
(Bonus: instead of jumping half way, you can estimate how far you need to jump.)
Example 3: Finding the number of unique items in a collection
Consider the array {10,70,20,20,20,90,10,90,20,70}. The four unique items are 10, 70, 20 and 90.
For an unsorted collection, you can choose to see if the item is first of its kind, and only if so, increase a counter.
For an sorted collection, every time an item is not the same as the next item, you can increase the counter (that is initialized to 1) by 1. Zero is returned for empty and null collections.
The second approach is signficantly easier than the first.
Sorting is good
Bottomline - It makes things MUCH easier!
Bogosort
Bogosort repeatedly shuffles the data until it happens to be in order. It is a fantastic way to waste time and highlights why we care about algorithmic complexity. A short implementation is given in BogoSort.java.
Tree sort
But we learned how to sort when we created tree structures!
Tree sort inserts every element into a binary search tree and then reads the values back by traversing the tree in order.
1
2
3
4
5
40
/ \
20 70
\ / \
30 60 90
The implementation can be found in TreeSort.java.
Cost of sorting
Of course, we haven’t considered the cost involved in sorting a collection. If the collection changes frequently, we need to maintain the sorting order. This can be done either by,
- adding the item that has to be added at the appropriate place (Which more or less requires one iteration through the collection) - pretty good!
- adding the item at the end and sorting the collection again - not so good.
What one must remember is that sorting is not free and has a cost associated with it.
Tree sort in particular stores every value in a node of a binary search tree. That extra memory can be significant and, if the data arrives already sorted, the tree degenerates into a linked list. In that worst case the insertions each scan most of the existing nodes giving an overall cost of $O(n^2)$.
Approaches to sorting
If I ask you to sort the collection, what would be your approach? Think about that for a few minutes and try to represent it as a flowchart.
{40, 70, 20, 90, 30, 80, 20}
One approach can be to find the smallest item and make sure it’s at the right place. That’s 20, and belongs at the first position (where 40 sits).
Sub-option 1
While putting it in its right place, we can either shift (one to the right) items before it and then place it at that location, so the collection becomes:
{20, 40, 70, 90, 30, 80, 20}
After this we are guaranteed that the first item is correct and continue with the rest of the collection, completely ignoring the first value.
Sub-option 2
Another option to put 20 in the right place is to simply swap it with whatever is there. Here, the collection becomes:
{20, 70, 40 90, 30, 80, 20}
Just like the first sub-option, we can totally forget about the first item once this is done, and carry on with the same process starting at the second item.
Full trace using “shifting” approach
Sorted part and unsorted part put in their own compartments.
40, 70, 20, 90, 30, 80, 20
40 70, 20, 90, 30, 80, 20
40, 70 20, 90, 30, 80, 20
20, 40, 70, 90, 30, 80, 20
20, 40, 70, 90, 30, 80, 20
20, 30, 40, 70, 90, 80, 20
20, 30, 40, 70, 80, 90, 20
20, 20, 30, 40, 70, 80, 90
Full trace using “swapping” approach
Sorted part and unsorted part put in their own compartments.
40, 70, 20, 90, 30, 80, 20
20, 70, 40, 90, 30, 80, 20
20, 20, 40, 90, 30, 80, 70
20, 20, 30, 90, 40, 80, 70
20, 20, 30, 40, 90, 80, 70
20, 20, 30, 40, 70, 80, 90
20, 20, 30, 40, 70, 80, 90
20, 20, 30, 40, 70, 80, 90
Bring it in!
Now that we’ve had an intuitive idea of what needs to be done, let’s formalize our understanding.
- The shifting approach is what is known as insertion sort.
- The swapping approach is what is known as selection sort.
Visualising different algorithms
https://sortvisualizer.fenilsonani.com/
Insertion Sort

See InsertionSort.java for a simple implementation.
Note that we can have variations of the same algorithm. For instance, the following version of insertion sort sorts in ascending order, starting the sorting process from right to left.

Selection Sort

The code in SelectionSort.java implements this approach.
Note that we can have variations of the same algorithm. For instance, the following version of selection sort sorts in ascending order, starting the sorting process from right to left.

Yes another version of selection sort sorts in descending order, starting the sorting process from right to left.

Bubble Sort
Bubble sort repeatedly swaps out-of-order adjacent items. While simple to understand, it is generally slower than insertion or selection sort. See BubbleSort.java for a demonstration.
Quick Sort
Quick sort works by choosing a pivot, placing smaller values before the pivot and larger values after it, and then recursively sorting the two partitions. A simple implementation is provided in QuickSort.java.
A worked trace on the numbers 40, 70, 20, 90, 30, 80, 20:
40, 70, 20, 90, 30, 80, 20
20 40, 70, 90, 30, 80, 20
20, 20 40, 70, 90, 30, 80
20, 20 30, 40 70, 90, 80
20, 20, 30, 40 70, 90, 80
20, 20, 30, 40 70 90, 80
20, 20, 30, 40, 70 80, 90
20, 20, 30, 40, 70, 80 90
20, 20, 30, 40, 70, 80, 90
Dual-Pivot Quick Sort
Dual-pivot quick sort extends the basic algorithm by selecting two pivots. Values less than the first pivot are placed on the left, those between the pivots stay in the middle and those greater than the second pivot move to the right. This reduces comparisons and is the approach used by Arrays.sort() for primitive arrays in Java.
A straightforward implementation can be found in DoublePivotQuickSort.java. The source file contains extensive inline comments explaining each step of the algorithm.
A simplified run on the same numbers with pivots 20 and 70:
40, 70, 20, 90, 30, 80, 20 20 40, 30 70, 90, 80, 20 20, 20 30, 40 70, 80, 90 20, 20, 30, 40 70 80, 90 20, 20, 30, 40, 70, 80, 90
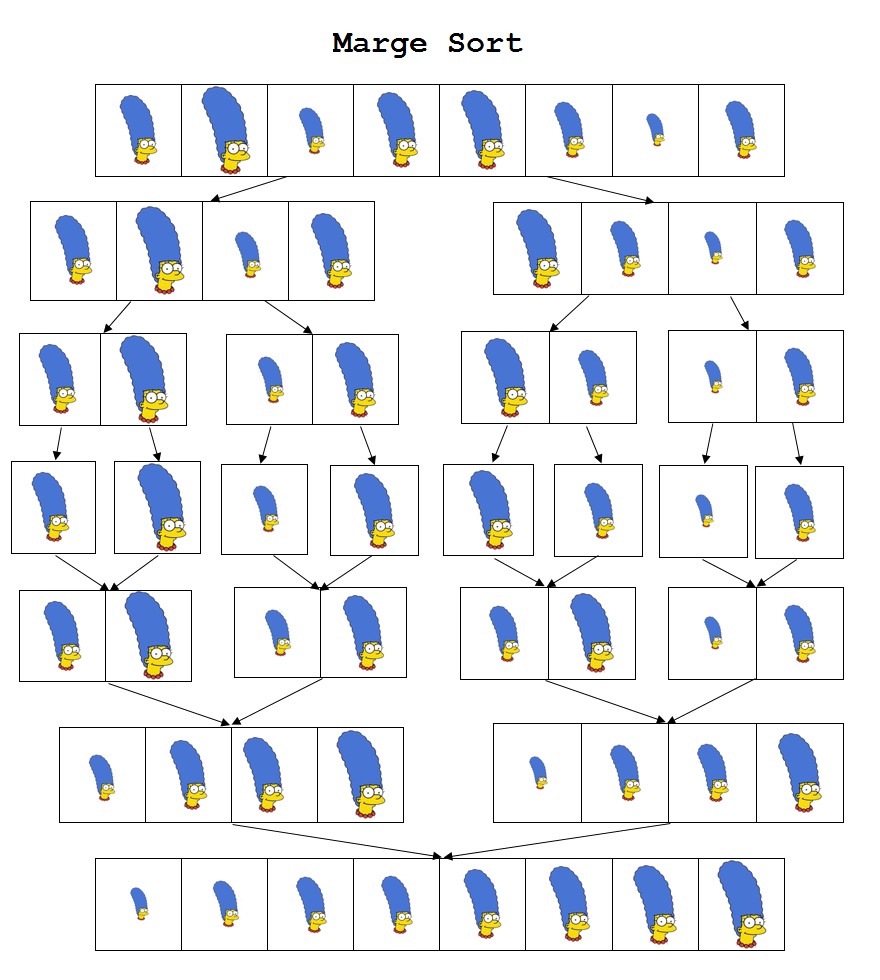
Timsort
https://sorting-visualizer.researchdatapod.com/
Timsort is a hybrid of merge sort and insertion sort. It is designed to take advantage of ordered subsequences in real data and is used by default when Java sorts objects.
A simplified run of Timsort on the same numbers identifies runs and merges them:
[40, 70], [20, 90], [30, 80], [20]
[20, 40, 70, 90], [20, 30, 80]
20, 20, 30, 40, 70, 80, 90
What’s the best we can do?
Comparison-based sorting algorithms can’t beat $O(n \log n)$ in the general case because each comparison yields limited information.
A comparison-based sorting algorithm only relies on comparing pairs of elements. Any such algorithm can be represented as a decision tree, where:
-
Each internal node represents a comparison between two elements.
-
Each branch corresponds to one of two outcomes ($\le$ or $>$).
-
Each leaf node represents one possible permutation (sorted order).
Step-by-step reasoning
-
Number of permutations: Sorting n distinct items could yield $n!$ possible outcomes.
-
Binary decision tree: A binary tree with height h has at most $2^h$ leaves.
-
Lower bound on height: Since you need at least as many leaves as possible outcomes, you must have: $2^h \ge n!$
-
Use Stirling’s Approximation:
For large n, Stirling’s approximation tells us:
$n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n$
Taking logarithms (base 2) of both sides:
$h \ge \log_2(n!) \approx \log_2\left(\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\right)$
This simplifies to: $h \approx n \log_2 n - n \log_2 e + O(\log n) \quad\Rightarrow\quad h = \Omega(n \log n)$
Exotic sort algorithms
To sort faster we need to look for more unusual approaches where we don’t compare numbers.
Sleep sort
Sleep sort launches a thread for each value and relies on the operating system’s timing to print numbers in order. It’s more of a curiosity than a practical algorithm. The code in SleepSort.java shows how it works.
Bead sort / Gravity sort
This method lets beads fall under gravity so that more beads collect on pegs for larger values. It only works for positive integers and illustrates how physical processes can be used to sort.
https://bead-sort.arithmetic.guru
Radix Sort
https://www.sortvisualizer.com/radixsort/
Radix sort processes the digits of numbers one position at a time, allowing integers to be sorted in linear time when the number of digits is limited. A full implementation appears in RadixSort.java.
A quick demonstration treats the digits from least significant to most significant:
41, 70, 21, 79, 26, 78, 21
(ones) 70, 41, 21, 21, 26, 78, 79
(tens) 21, 21, 26, 41, 70, 78, 79
Quantum acceleration?
It remains an open research question whether quantum computers can achieve more than a constant factor speed-up for sorting.
Sorting in the Java standard library
Java provides Arrays.sort() to sort arrays and Collections.sort() for lists.
Arrays of primitives use a tuned Quicksort while object arrays and lists are
sorted with Timsort. Example usage:
1
2
3
4
5
int[] data = {40, 70, 20};
Arrays.sort(data); // in-place
List<Integer> list = new ArrayList<>(List.of(40, 70, 20));
Collections.sort(list);
Comparable and Comparator
List.sort() and Arrays.sort() rely on comparison logic rather than the < or > operators. If an object does not provide a natural order, Java offers two ways to supply one.
Comparable
Implement Comparable<T> to define how instances compare:
1
2
3
4
5
6
7
8
9
public class Person implements Comparable<Person> {
String name;
int age;
@Override
public int compareTo(Person other) {
return Integer.compare(this.age, other.age);
}
}
Instances can then be sorted without extra arguments:
1
2
3
4
List<Person> people = ...;
Collections.sort(people); // uses compareTo
people.sort(null); // also uses compareTo
Arrays.sort(personArray); // also uses compareTo
Comparator
If the class does not implement Comparable or a different order is required, supply a Comparator<T>:
1
2
people.sort(Comparator.comparing(p -> p.name));
Arrays.sort(personArray, (a, b) -> a.name.compareTo(b.name));
Under the hood
- A
ComparableorComparatormust be available. - The sort methods call comparison functions instead of
<or>. - Object sorting uses dual-pivot quicksort for
Arrays.sort()and TimSort forList.sort(). - Without a comparison strategy, a
ClassCastExceptionoccurs.
Primitive arrays still use < and > directly with an optimised quicksort.
In short, objects must be comparable—either naturally or via a comparator—otherwise sorting fails at runtime.
Sorting Unicode strings
Java sorts Unicode strings using lexicographic order based on UTF-16 code units. Methods like Arrays.sort(String[]) or Collections.sort(List<String>) rely on String.compareTo(String).
1
2
Arrays.sort(strings);
Collections.sort(stringList);
String.compareTo compares characters one by one using their UTF-16 values. This works but ignores language conventions:
1
2
"apple".compareTo("banana"); // negative -> "apple" < "banana"
"\u00E4".compareTo("z"); // negative -> "ä" < "z"
In German, ä would typically appear near a, so the default order may seem strange.
Locale-sensitive sorting
Use Collator for proper Unicode-aware ordering:
1
2
3
4
5
6
import java.text.Collator;
import java.util.*;
Collator collator = Collator.getInstance(Locale.GERMANY);
List<String> words = Arrays.asList("äpfel", "apfel", "zebra");
words.sort(collator);
A Collator handles accents, case differences and language-specific rules. Its strength can be tuned:
1
collator.setStrength(Collator.PRIMARY); // ignores accents and case
Summary
| Approach | How it sorts | Use case |
|---|---|---|
String.compareTo() |
Lexicographic by UTF-16 code unit | Fast, binary-safe sort |
Collator |
Locale-aware Unicode sorting | Human-friendly alphabetical order |
If you rely on compareTo(), strings are ordered by raw Unicode values. Use Collator when you need natural alphabetical sorting.